“It must be fictitious!” Aeroperu 603
On the 2nd of October in 1996, Aeroperú 603 made history with a frantic and heartbreaking 25-minute flight that ended with the loss of the aircraft and all on board. This accident highlighted the importance of the pitot-static system and the effects of spatial disorientation in a way that is hard to over-emphasise. With the loss of Lion Air flight 610 last week, which seems to be related to AoA and unreliable speed indications, Aeroperú flight 603 is being referenced in aviation forums and opinion pieces as a similar crash.
I’m not sure Aeroperú 603 does a lot to help us understand the Lion Air crash. Lion Air’s Boeing 737 had an angle of attack indicator which the Boeing 757 did not have, the Lion Air flight happened during the day in daylight and clear weather whereas the Aeroperú flight took place at night and in cloud. Nevertheless, I think it’s worth looking at what happened that night and the critical factors of airspeed, altitude and angle of attack in flight.
Aeroperú flight 603 was a scheduled passenger flight which departed Miami on Tuesday the 1st of October for Santiago, Chile, with a planned stop at Jorge Chaves International Airport in Lima, Peru’s main international and domestic airport.

The aircraft for the flight to Santiago, a four-year-old Boeing 757-23A, had suffered a bird strike, including ‘avian ingestion’ into the right engine, and required repairs. The maintenance team at Lima replaced two turbine blades (damaged by the birds sucked into the engine) and repaired the hydraulic pump. The last stage was to clean and polish the lower front part of the fuselage. This was done by a line mechanic, who started by covering the static ports with masking take to make sure that none of the polish or other foreign material would interfere with the air intake.
The pitot-static system is critical to flight. The pitot measures the dynamic air pressure and the static ports measure the static air pressure: between them, they feed the altitude and the airspeed to the flight crew. It is vital that they are protected from contamination.
So, the line mechanic covered the static ports with masking tape to protect them and then he cleaned and polished the fuselage, as per his instructions. He should have removed the tape when he finished but somehow, he didn’t. The standard procedure is that a Quality Control staff member supervises the finishing of the job. Responsibility for the aircraft then goes to the duty supervisor who then hands over the aircraft to the line chief. The line chief then hands it over to the pilot responsible for the flight, in this case the captain. The tape was a dull silver colour and the static ports are high off the ground; none of the people who should have been involved in the handover noticed that the tape had not been removed. Finally, the pre-flight checks included the specific task of checking that the static ports were clear; however when the captain did his walk-around, he never noticed the tape.
The flight crew prepared for take off. There were seven cabin crew and sixty-one passengers for the flight to Santiago. The Boeing 757 took off from runway 15 just after midnight local time.
As they climbed away, the first officer called for the landing gear to be retracted. Instinctively checking their height at this point, he realised there was something wrong. The altimeter appeared to be stuck.
As he called out, he was interrupted by the wind shear alarm which sounded three times. The wind shear alarm is to warn the flight crew of a sudden change in wind speed or direction, for example a microburst. Effectively, it means that you are heading through an unpredictable set of fast winds.
The captain warned the first officer, the pilot flying, to keep his airspeed up. Then he asked if they were descending, while the first officer insisted that he was climbing. The captain attempted to notify ATC but then he was interrupted by the rudder ratio alarm. The rudder ratio alarm means that the pilots need to avoid any abrupt rudder inputs.
As the alarms blared, the captain reiterated that they did not appear to be climbing properly. The first officer, as pilot flying, knew that he had put the power on and had the aircraft pitched up for a climb. He was more worried about the the low indicated airspeed, which would be made worse by increasing his climb rate. He briefly levelled out the aircraft to gain more airspeed and then continued the climb. ATC watched the Boeing disappeared into the clouds.

At the same time, the captain tried to find out why the rudder ratio alarm was sounding while the first officer looked at the source selector, which was exactly the right thing to do in the case of a blocked static port. This changes the source, using a different static port, which should reinstate access to correct altitude and airspeed data. However, in this case it made no difference because all of the static ports had been taped up. Worse, the ports were only partially blocked. A stuck altimeter is easy to ignore but one that appears to be responding is more difficult to make sense of.
The mach trim warning started to sound, which means that the airspeed is too high and the stabiliser has stopped functioning. The rudder ratio alarm was still sounding. The captain called for them to go to basic instruments, again, the right thing to do in the case of unreliable air data caused by a blocked static ports.
At the same time, the first officer declared an emergency to ATC. At this stage, they were unsure of their height, their speed, the state of their rudder and the state of their stabiliser. They were flying through a low layer of cloud at night with no visual references. If they made the wrong decision, they knew it could be fatal. If they didn’t take a decision, they knew it would definitely be. Not doing something was the worst course of action, they had to do something. But what?
Jorge Chavez International Airport had a radar surveillance system which was being tested, so the controller asked them to switch frequencies so that they could offer radar advice and support.
The captain took control of the Boeing 757 while the first officer coordinated with ATC for a return to the airport using the Instrument Landing System (ILS). Meanwhile, they both continued to try to make sense of what was happening.
The flight crew took the aircraft out to sea, so that they wouldn’t have to worry about the terrain; just north of Lima were the foothills of the Andes. By climbing away over the sea, they would gain some time and space to troubleshoot and safely return to the airport.
The first officer asked the air traffic controller for the aircraft’s flight level and speed. The radar controller confirmed that they were at 4,000 feet. This must have been a great relief to the flight crew, as it corresponded to what the altimeter was showing. They focused again on the rudder ratio and their airspeed, which still appeared to be low.
But the controller was using secondary radar, which means that he was picking up the airspeed and altitude information from the aircraft’s transponder. Rather than confirming their height, he has simply repeated the same altitude information that their instruments were showing them. The partially blocked static ports were not able to measure their altitude correctly and so the information displayed on his radar was just as wrong as it was in the cockpit.
However, now that the crew believed that they had independent verification of their height above sea level, they stopped worrying about their altitude and focused on the other systems.
They continued to climb. The first officer then asked the controller again to confirm their airspeed and their altitude. Those are the two parameters needed for safe instrument flight. The controller responded that they were currently climbing through 6,000 feet. The first officer said that their altimeter showed 7,000 feet and the controller confirmed that was correct: “Now reading seven zero.”
It didn’t occur to anyone that they were all referring to the same faulty data and the controller did not respond in regards to their ground speed, which is measured independently by the radar system.
They couldn’t use the autopilot, which was receiving the same bad data that they were. The first officer told the controller that they had control problems. There was no reason why the aircraft should have been handling badly, so this must was probably a reference to the rudder ratio and mach trim alarms.
Earlier that same year, another Boeing 757 suffered these same inexplicable warnings. In that case, the NTSB investigation concluded that the pitot-static system had failed because of a wasp’s nest built in the pitot tube, obstructing it. They recommended that the 757 flight manual include the information that if the rudder ratio and the mach trim alarms go off at the same time, it’s a symptom of an airspeed discrepancy and likely a failure of the air data. However, as it had only happened once, this information was not disseminated as a matter of urgency and the Aeroperú flight crew had no idea.
The captain wanted to find out what was wrong with the aircraft and solve it, if possible, before returning to intercept the localiser on the ILS, the Instrument Landing System. An Instrument Landing System is based on airport runway information being transmitted from the ground and received in the cockpit, so the data is not affected by the faulty systems on the aircraft. It consists of a localiser and a glide slope. If they could intercept the localiser, they would be able to follow the glide slope to bring them down.
In the cockpit, they worked through what seemed to be the relevant checklists while climbing to 12,000 feet out to sea. The first officer checked the alternate air again, unable to believe what the instruments were showing…but again, because all of the ports were partially blocked, it did not help. They were unable to make sense of the warnings or stop the alarms from sounding.
He pressed the captain to stop troubleshooting and to return the airport. The captain wanted to stay high over the water where they were safe and work out what was wrong. They were both right and they were both wrong.
The first officer asked ATC for assistance with altitudes and speed until they could be guided to the localiser. It was clear to both of them that their instruments couldn’t be trusted.
Air Traffic Control gave them a new heading to turn them back towards the airfield with full instructions, just in case they lost radio communications. The controller told them that next they would turn right to intercept the localiser with an initial descent to 4,000 feet.
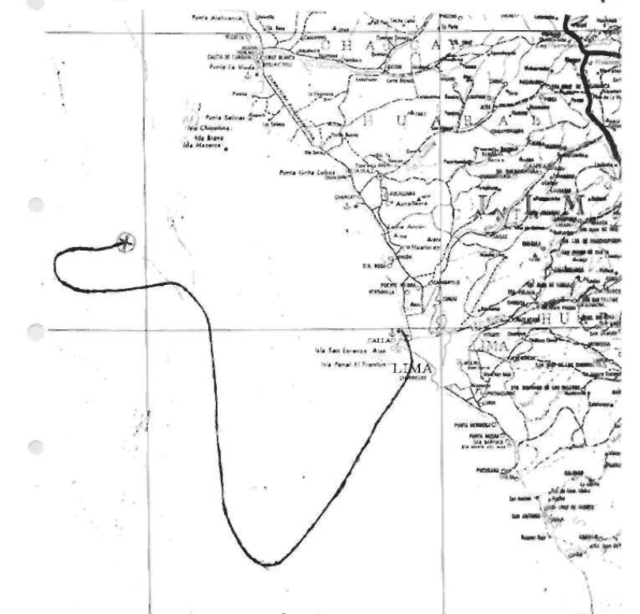
The flight crew followed the vectors from ATC and attempt to set up for a landing with no Flight Director, no auto-pilot and no auto-throttle.
As they began their descent, the displayed airspeed started to increase rapidly. The overspeed warning sounded. This is another warning which needs immediate attention and action. It means that they were going over the structural and engine tolerance limits: the aircraft was going faster than Boeing deemed safe for a 757.
It is worth considering that all of this is happening over the course of a few minutes. It was clear to the crew that not all of the alarms could be correct. Both pilots expressed disbelief that their speed was still increasing after they had reduced the thrust and put the speed brakes on. The rudder ratio alarm sounded again. Both pilots stated at different points that the air data must be wrong: the first officer called out for alternate air and the captain advised that they should use only ‘basic’ instruments. But nothing helped to shed light on what was happening. They couldn’t see out and they couldn’t trust their senses. Nothing was obvious.
ATC confirmed that the aircraft was 31 miles west of the airport at just over 10,000 feet with a speed of 270 knots over the ground. This was the first time that ATC had given the flight crew their groundspeed. Meanwhile, the cockpit display showed an airspeed of 350 knots.
Ground speed is, as it says, the speed you are travelling across the ground. Airspeed is how quickly you are moving through the air. The performance of an aircraft is affected by the speed that the aircraft moves through the air; it is critical for the aircraft’s Angle of Attack. If your aircraft is about to stall and you aren’t able to reduce the angle of attack, you will crash. A common cause for a stall is that the airspeed is too low: the wings lose lift and it doesn’t matter one bit what your groundspeed is, your aircraft will stop flying. On the other hand, if your airspeed gets too high, it can cause fatal structural damage to the aircraft.
In both of these cases, your ground speed is not relevant. However, if you know the wind direction and speed as well as the aircraft’s ground speed, you can work out something close to your current airspeed. Unfortunately, by now the flight crew were so overloaded, they couldn’t deal with this additional information.
Reassured by the radar controller that they were at 10,000 feet, they continued their descent. The overspeed alarm sounded again and continued to sound, even though they’d reduced the thrust and activated the air brakes.
Then the stick shaker activated, the control columns vibrating violently. This indicates a high angle of attack, which means that the aircraft is in danger of stalling. The captain stopped their descent in order to gain time to think.
In the Boeing 757, the stick shaker is triggered by the actual air flow (or lack of it, rather), over the wings. This is physical evidence and unaffected by the air data. If the flight crew had understood that, or at least had a moment to think clearly, they would have realised that this meant the overspeed warnings were incorrect and could be disregarded. But with five different alarms sounding and chaos in the cockpit, they never made that connection. As far as they were concerned, the Boeing 757 was either flying dangerously slowly or overspeeding. Both alarms were urgent, both required action, but which one was true?
The first officer asked for another aircraft to help them understand the situation. If someone could fly alongside, that would help them determine whether their airspeed was dangerously high or critically low. It would also confirm their altitude.
The flight crew did not know it but the aircraft had entered a gentle descent. The altimeter was not changing and the controller repeatedly confirmed their altitude, so they believed that they were flying straight and level.
The controller told them that they had another aircraft almost ready for take-off that would come and fly with them as a guide plane but it would take another 15 minutes.
Despite the descent, the stick shakers activated again, vibrating their control columns. The overspeeding alarm continued to sound, along with the mach trim warnings and the rudder ratio alarm. It must have been a nightmare trying to think straight.
The captain believed the overspeed warning while the first officer was convinced that they were stalling. Both of them believed that they were safely at 9,500 feet.
The next alarm to sound was the Ground Proximity Warning System, calling out TOO LOW, TERRAIN, TOO LOW, TERRAIN. This contradicted the one piece of information that they had confirmed as correct. The warning sounded twenty-two times over 45 seconds. The captain believed that they must have inadvertently overflown the coastline and heading into the mountains of the Andes, where he knew the terrain swiftly rose to ten thousand feet. The first officer called ATC who said that no, radar showed them as out to sea and at FL100, that is, 10,000 feet.
However, the Ground Proximity Warning System uses the radio altimeter, not the barometric altimeter. The radio altimeter is specifically useful for low level flight, as it bounces off the ground to give you your true height above terrain. Once the radio altimeter responds, which means you have descended below 2,500 feet above the ground, the Ground Proximity Warning System will sound if the aircraft is not configured for landing.
This meant that they now had three references to information that they could trust: their groundspeed as picked up by radar, their altitude as measured by the radio altimeter and the stick shaker demonstrating that their angle of attack was approaching stall point.
However, they were so bombarded with information that they were unable to make sense of this data. The cockpit resource management (CRM) had completely fallen apart and the flight crew were not acting as a team. Instead, they argued about what instruments to believe. They referred to the checklists over and over again, even though there was clearly nothing there that can help them.
And they were no longer competently flying the plane. The Boeing 757 entered a gentle climb, taking them above 2,500 feet. The Ground Proximity Warning System stopped sounding. As far as the (barometric) altimeter was concerned, they’d been flying straight and level the entire time, so the flight crew saw this as confirmation that the GPWS warning was wrong, or ‘fictitious’ as the captain put it. The flight crew clearly did not have sufficient training to diagnose the problem and recognise the true indications against the false ones.
All of the alarms and warnings could not be true; some of them must be based on unreliable data. Unfortunately, the captain chose exactly the wrong warning to call fictitious.
With low airspeed and the aircraft in a climb, the aircraft suddenly dropped 700 feet; a stall. The SINK RATE alarm sounded. The Ground Proximity Warning System sounded as they dropped below 2,000 feet above the water.
The flight crew intentionally put the aircraft into a climb this time. However, they were still unaware of their previous descent and gentle climb. Based on the FDR data, the aircraft climbed to 2,400 feet and then descended to 1,300 feet and then climbed again to 4,000 feet and levelled out. Throughout these manoeuvres, the altimeter showed that they were above 9,000 feet. The controller confirmed it.
Ready for the attempt to intercept the localiser for the instrument landing system, they turned.
The overspeed warning continued to blare although they had reduced the thrust to idle. TOO LOW, TERRAIN sounded again in the cockpit and continued to sound. The first officer asked for the controller again to confirm their altitude, clearly struggling to believe what he was being told. The controller reported that they were at 9,700 feet.
Desperate to get the aircraft onto the ground, they descended again, ignoring the Ground Proximity Warning System. From 4,000 feet above sea level, they began their 5,700 foot descent to intercept the ILS.
Suddenly, the lights of the Boeing must have illuminated the dark waves of the sea. The aircraft touched the water and the first officer cut off his call to the controller to shout pull up, pull up! The controller also shouted after hearing the warning sounds in the cockpit. “Go up, go up if it indicates pull up!” This was the first indication that the Ground Proximity Warning System should be trusted over the radar information that he had been giving them. The captain pulled up and the GPWS warnings stopped. But it was too late; with idle thrust and already dangerously slow, the speed decayed to nothing. The captain realised he’d lost control of the aircraft, saying just ‘we are going to invert’ as the wing dropped and the Boeing banked left. There was nothing he could do to recover.
As they crashed into the water, the captain’s instruments showed that their airspeed was 450 knots and the altimeter still read 9,700 feet above sea level. Only in the last seconds would the passengers have been aware, as the previous climbs and descent were too gentle to be felt, even in the cockpit. They, like the flight crew, could see nothing out of the windows other than the black night and the lights of the wings reflecting off the cloud. The cabin crew, unprepared for the emergency, could not offer any help. There were no life jackets nor life rafts for the passengers.
The aircraft plunged into the water and sank. The winter water temperatures were likely near to freezing; anyone who survived the impact and escaped the cabin would have had less than 15 minutes in those temperatures before falling unconscious or collapsing with exhaustion. However, it’s unlikely that anyone made it out of the aircraft at all.
The fog never lifted and the seas were rough. By the following evening, rescue workers had recovered only ten bodies. There were no survivors.
The conversation from the cockpit voice recorder was released and can be heard online. But be warned, it is harrowing to listen to, even if you don’t speak Spanish.
Investigators could not recover the aircraft; however underwater photography proved that the captain’s static port was blocked by tape. It wasn’t hard to follow the trail from there and understand what had happened.
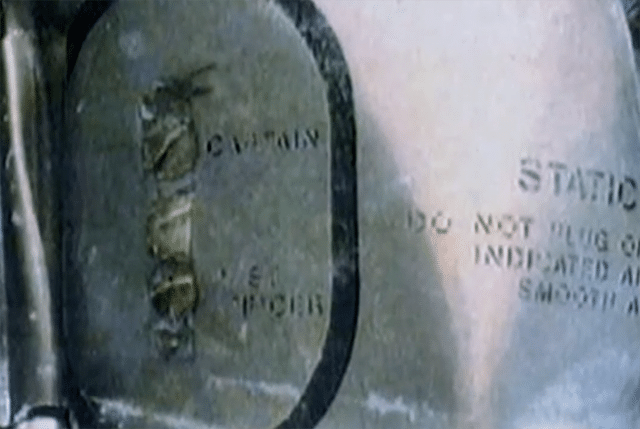
From an unofficial translation of the accident report by the Peru Ministry of Transport:
It can be deduced from the investigation carried out that the maintenance staff did not remove the protective adhesive tape from the static ports. This tape was not detected during the various phases of the aircraft’s release to the line mechanic, its transfer to the passenger boarding apron and, lastly, the inspection by the crew responsible for the flight (the walk-around or pre-flight check), which was carried out by the pilot-in-command, according to the mechanic responsible for the aircraft on the day of the accident.
The pilot-in-command made a personal error by not complying with the procedure for GPWS alarms and not noticing the readings of the radio altimeters in order to discard everything which he believed to be fictitious.
The co-pilot made a personal error by not being more insistent, assertive and convincing in alerting the pilot-in-command much more emphatically to the ground proximity alarms.
In the aftermath, Aeroperú filed for bankruptcy while Boeing paid compensation to the families of the victims, taking responsibility for failing to train pilots to deal with this circumstance rather than for the disaster itself. The static ports being covered were, Boeing said, a clear case of careless maintenance followed by a negligent pre-flight inspection by the captain.
The line mechanic was convicted of negligent homicide.
References:
* Final Report by La Comision de Investigacion de Accidentes
* Unofficial English translation
* Close-Up: Aeroperu 603 Voice Recorder Transcription (English Translation)








Pitot tube covers, control surface motion limiters, and other ground-only safety locks always have a highly visible tag or banner attached. I recommend that when tape is used, the end of a strip of brightly colored ribbon should be inserted under the last few turns of tape allowing the ribbon to hang down to serve as a safety tag.
My first thought was that the tape itself should have been in a contrasting color; I’d think an assorted set of gaffer’s tape (no-residue tape used to hold down lighting cables in theaters) would be easier to keep on hand than ribbons in contrasting colors. (A long-enough ribbon might not need to be contrasting, but would get in the way of work.) But there certainly should have been \something/ making the covering more apparent.
Things are different now; here’s a description by a mechanic: According to our company procedure, the cleaners notify us that they need to do an external wash on aircraft XYZ. We cover the static ports using a bright red self-adhesive plasic tape, to which we attach long flags (appr. 1 metre) of red and white danger tape. Additionally a laminated card stating “CAUTION! STATIC PORTS COVERED!” will be attached to the captain’s steering wheel. Then a tech log entry stating that the static ports have been covered is made.
At the time, it depended on the operator (although I don’t think there was anywhere that specifically advocated using dull grey tape!)
The wrong tape was actually used. The procedure called for bright highly reflective tape. The mechanic couldnt find any, and instead decided to use regular gray duct tape.
Well, sure you can put a strip of bright ribbon on the tape, but then you can also remember to take the tape off. I feel if someone’s conscientious to do the ribbon, then they’re the type to just remember to pull the tape off. Plus that does seem to be fairly obvious tape. I don’t think the pilot even really looked at it.
I do not agree with the accident report findings. The plane was lost long before the GPWS alarms.
I think the radar controller was far more at-fault than even the mechanic. By grossly misleading the flight crew with incorrect information, he destroyed any hope of troubleshooting things and made them believe the incorrect instrument readings. When the stick shakers went off, I’m sure they felt they were drowning in a sea of conflicting information.
It became standard to use contrasting tape after this (usually applied as a big X), to at least to allow someone further down the chain a chance to spot the issue. The radar facility was new; I don’t know if the controller was badly trained, hadn’t paid attention or just happened to get thrown into the situation because he was there that night. But yes, it’s frustrating to see him confirm, over and over again, that they are at a safe height.
A controller can only give the information he can see on his screen; he did not know what problems the crew had and seems to have only been told about control problems, nothing else. I cannot see why you wish to blame the controller, he had no idea that his information could be wrong. If the controller had tried to second guess anything about the information he was giving to the crew, then he may very well have given them totally wrong information and confused the situation even further.
The controller should know where the information on their screen originates: which part of it originates with local sensors (and what their capabilities are), and which part originates with aircraft sensors and is transmitted to the ground. Understanding the system you are working with is the result of training; if the understanding of the operator is incomplete, they were badly trained.
There is no need to second-guess anything in this scenario, all it needs is the knowledge which information comes from local sensors and which does not.
If you’re smart enough to try to contact the Navy at Callao, you are more than smart enough to (a) know that when your GPWS activates, you had better gain altitude, (b) know that your aircraft has a stick shaker that works independently of the pitot system, and (c) know how to use a farking radar altimeter (regardless of how the GPWS works). The pilots were overwhelmed and hyper-stressed. Were they to be reading of a similar accident before their own flight, they would have certainly known what to do. I think they just freaked out. Neither one had enough certainty and immediate recollection of knowledge to convince the other crew on deck what a good procedure would be (including why, so there would be trust). In the end, the technician and command pilot both failed, but the tech failed to even care properly whereas the command pilot simply failed to be as good as we would all hope we could be.
Whoops, responded to the wrong guy.
The airport is very close to the Callao port, where the Peruvian Navy is based. My question is: would an air defense system from a warship be able to get better, precise data? Could that have been a backup? It’s only one radio call away.
Sylvia — “This indicates a low angle of attack, which means that the aircraft is in danger of stalling” seems wrong; a stall happens when the angle of attack is too high. Also, was the artificial horizon not usable, or was there no mention of checking this on CVR? IIRC the gyros don’t depend on the static port.
This is interesting because it shows a point failure, unlike most of your cases where a lot of errors piled up to cause a crash. It can be argued that the crew should have handled the problems better — but I wonder whether this kind of instrument failure is included in any simulation, as it seems unusual.
GAH! Yes, dammit, I started talking about airspeed and then realised that was wrong and changed it without noticing that it still said it was low. I’ve now corrected the text, thank you!
There’s no reference to the artificial horizon but I wondered if the gentle climb/descent were such that it wasn’t easy to see the pitch change. But it is clear that the crew weren’t able to focus on the instruments that were trustworthy. The report refers to ‘tunnel vision’.
This type of failure is definitely included in modern sim training. At the time, though, I suspect it wasn’t.
Does this not make a case for a GPS? I know this does not give airspeed, but with altitude and ground speed, one can work out airspeed and by watching altitude change, get at least a rough idea of AoA? Independently. The controller was also seriously at fault. But a super scary story.
Yes it does, in fact. In a modern aircraft, you would have your groundspeed available throughout and having just taken off, you could probably work out your airspeed fairly quickly. Also, modern Boeings have a specific sensor for testing AoA (which is at the heart of the Lion Air investigation right now).
The copilot can be heard calling out speed during the takeoff roll. What was he reading it from?
I’ve read the article again and I realised that they did have the speed readings, just wrong ones – the indicated airspeed was higher than the real airspeed. Does it mean that they took off at a speed lower than usual? If so, why didn’t they notice that?
Modern aircraft all have navigation systems based on GPS.
Older aircraft have them retrofitted because the old navigation from beacon to beacon is long obsolete. Today it is nearly impossible to make a flight plan without having access to computer systems that also integrate with ATC because airspace is so crowded, parallel routes are used between GPS-based waypoints.
ATC cannot really be blamed, their information as Sylvia’s article demonstrated came from the same source the aircraft’s transponder. And that, in turn, got it’s data from the Air Data Computer which (in this unfortunate chain) was in turn getting false information.
As H_E mentions: the mystery is what speeds were shown during take-off? As he aircraft was still accelerating on the ground, the ports would still have recorded the ambient pressure and speed read-outs must have been close enough to normal not to cause alarm:
During the nightmare scenario that developed the pilots were obviously totally overloaded. I know a few pilots who may have had the skills to work it all out, they were test pilots. They were selected from the very best and were used to, indeed were highly trained to cope with extreme situations. But most probably would have lost control of the situation.
I agree that it should be mandatory to use a highly visible contrasting colour if the ports must be masked off. And a procedure, where a ground crew MUST notify a responsible member of the engineering staff before masking off the ports should be mandatory too..
I understand airplane GPS systems not reporting airspeed; they can’t, without the information that was already blocked. However, can they report groundspeed, or is that considered a distraction? (The handheld automobile GPS that I inherited reports groundspeed, AFAICT more accurately than my speedometer, but I can see situations in which the difference between groundspeed and airspeed would be big enough to be a problem.) It does seem to me that ATC shouldn’t be telling the pilots airspeed, since that’s secondary info; it’s not clear whether ATC radar is precise enough to determine groundspeed, but even if it were there’s still the problem of the difference from airspeed (which governs whether the plane flies or falls).
I agree with Sylvia!
I still remember my dad waking me up early that morning and telling me that my uncle’s plane had an accident. He was David Fernández, the co-pilot.
I’ve never been able to fly without picturing what they went through in that cabin.
My family has had the recording of the CVR for 20 years and it took me this long to build up the courage to listen to it. I can’t believe I would find it on YouTube.
I shivered through the entire recording hearing my uncle’s voice, I cried the last few minutes, not quietly.
I miss him very much.
The recording is hard to listen to, even for a complete stranger. I’m sorry for your loss. What happened to your uncle and everyone on that plane was terrible and should never have been.
It is a nasty failure – losing static data. Because it’s basically never trained, contrary to unreliable airspeed. Also because there’s immediately a partial loss of situation awareness (altitude) and a risk of greater loss of situation awareness – as tragically demonstrated by this accident. You can fairly easily control your flight path without reliable airspeed indications. Without barometric altimeters, however, it seems more complicated to understand the overall situation (for instance, the fact that the transponder is using static data too…). Conflicting warnings and ensuing loud noise increase the stress level and the workload, making things even worse.
Not a pleasant situation.
It is so sad that the one thing they felt they could rely on, their altitude reading was faulty. It must have been a relief when they thought they were high enough to work out the rest of the issues, then, too late, they discover that they are not. Not knowing which information to trust and which to discard, not realizing they could not trust air traffic control, not having visual data, was a perfect storm. Why were they not trained to fly and land the plane in the event that the high tech computer systems failed them? Why so much reliance on computers to the point that human pilots are secondary? While these big corporations like Boeing work out the kinks of their most high tech planes, I imagine that more incidents like this will occur. Some might say that if it had not been for human negligence the computers would have worked fine. That is true. But still, humans need to know how to take over in the event that “any” issue causes the computers to give false information. I think Boeing needs to care more about human beings and less about being the most advanced corporation around!
To be fair, it wasn’t a “high tech system” that failed, but the simple, tried and true pressure altimeter.
The high-tech radar altimeter was working and could have saved them.